©2026 数学クラブ http://sugaku.club/
月 日( )
● 正三角形の定理を使った証明 [2K2-z0]
|
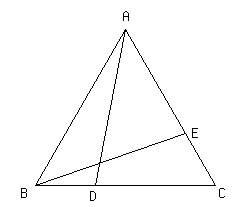
正三角形ABCの辺BC,CA上にそれぞれ点D,Eがあります.BD=CEであるとき,∠BAD=∠CBEになることを証明しなさい.
 |
©2026 数学クラブ http://sugaku.club/
月 日( )
【解答例】
|
正三角形ABCの辺BC,CA上にそれぞれ点D,Eがあります.BD=CEであるとき,∠BAD=∠CBEになることを証明しなさい.
 △ABDと△BCEで 仮定より BD=CE ---① △ABCは正三角形だから, AB=BC ---② ∠ABD=∠BCE=60° ---③ ①②③より,2組の辺とその間の角がそれぞれ等しいので △ABD≡△BCE 合同な図形では,対応する角は等しいので ∠BAD=∠CBE |