©2026 数学クラブ http://sugaku.club/
月 日( )
● 直角三角形の定理を使った証明 [2L4-z0]
|
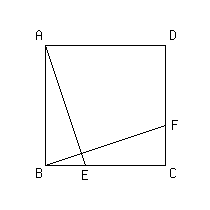
正方形ABCDの辺BC,CD上に,AE=BFとなる点E,Fがあります.このとき,BE=CFであることを証明しなさい.
 |
©2026 数学クラブ http://sugaku.club/
月 日( )
【解答例】
|
正方形ABCDの辺BC,CD上に,AE=BFとなる点E,Fがあります.このとき,BE=CFであることを証明しなさい.
 △ABEと△BCFで 仮定より AE=BF ---① 四角形ABCDは正方形なので AB=BC ---② ∠ABE=∠BCF=90° ---③ ①②③より,直角三角形の斜辺と他の1辺がそれぞれ等しいので △ABE≡△BCF 合同な図形では,対応する辺は等しいので BE=CF |