©2026 数学クラブ http://sugaku.club/
月 日( )
● 平行四辺形の定理を使った証明 [2M3-z0]
|
次の図で,△ABC≡△EDF,AC//EFならば,四角形BHDGは平行四辺形であることを証明しなさい.
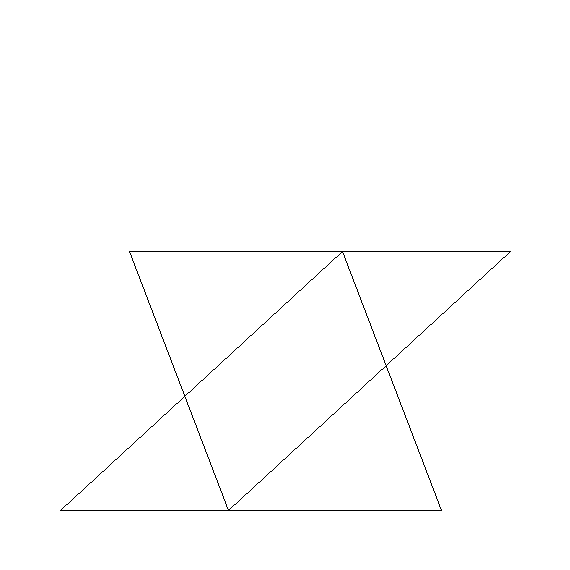 A B C D E F G H |
©2026 数学クラブ http://sugaku.club/
月 日( )
【解答例】
|
次の図で,△ABC≡△EDF,AC//EFならば,四角形BHDGは平行四辺形であることを証明しなさい.
 A B C D E F G H ∠A=∠FBG ---① ∠F=∠GDA ---② △ABC≡△EDFより,合同な図形では 対応する角の大きさは等しいので ∠E=∠A ---③ ∠F=∠C ---④ ① ③ から,∠E=∠FBG ---⑤ ② ④ から,∠C=∠GDA ---⑥ 同位角の等しい2直線は 平行なので ⑤ から,DH//GB ---⑦ ⑥ から,BH//GD ---⑧ ⑦ ⑧ から,2組の向かい合う辺がそれぞれ平行なので,四角形BHDGは 平行四辺形である. |