［文字サイズの変更］▼▲
 
©2024 数学クラブ http://sugaku.club/
月     日（     ） 
● 平行線と線分比の証明２      [2Y2-00]
(1) 次の図で，l//m//n ならば BC:AB=EF:DE であることを証明しなさい．ただし，直線b'はAを通り直線bに平行な直線である．
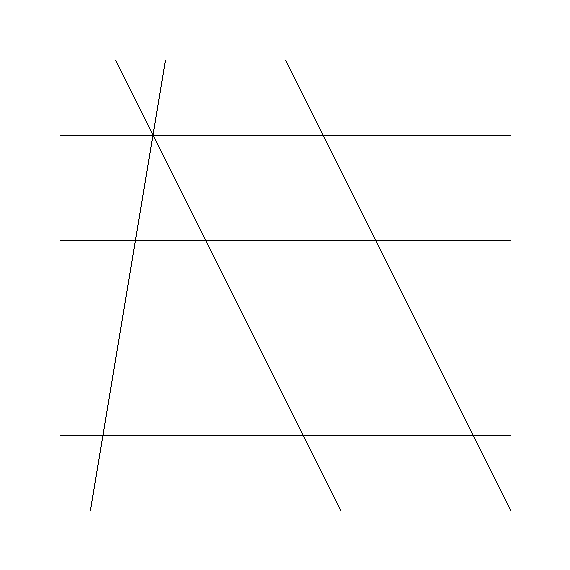A
B
C
D
E
F
G
H
l
m
n
a
b'
b
 
 
©2024 数学クラブ http://sugaku.club/
月     日（     ） 
【解答例】
(1) 次の図で，l//m//n ならば BC:AB=EF:DE であることを証明しなさい．ただし，直線b'はAを通り直線bに平行な直線である．
A
B
C
D
E
F
G
H
l
m
n
a
b'
b
△ABGと△ACHにおいて
仮定m//nより，同位角は等しいから，∠ABG＝∠ACH，∠AGB＝∠AHC
２組の角がそれぞれ等しい ので，△ABG∽△ACH
相似な図形では，対応する辺の比は等しいので
 AC：AB
 
 =AH：AG
 
 AB＋BC：AB
 
 =AG＋GH：AG
 
AB＋BC
 
 
AB
AG＋GH
 =
 
AG
BC
 
 
AB
GH
 =
 
AG
 BC：AB
 
    ---①
 =GH：AG
 
仮定l//mより  AD//GE  また，  AG//DEから四角形AGEDは平行四辺形であり，向かい合う辺の長さは等しいので
    AG＝DE    ---②
同様に，GH＝EF    ---③
①②③より
    BC:AB=EF:DE