［文字サイズの変更］▼▲
 
©2024 数学クラブ http://sugaku.club/
月     日（     ） 
● 二等辺三角形の定理を使った証明      [2i2-z0]
二等辺三角形ABCの底角∠B，∠Cの二等分線の交点をDとするとき，DB＝DCであることを証明しなさい．
 
 
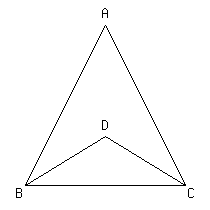©2024 数学クラブ http://sugaku.club/
月     日（     ） 
【解答例】
二等辺三角形ABCの底角∠B，∠Cの二等分線の交点をDとするとき，DB＝DCであることを証明しなさい．


仮定より
     1     ---①
 ∠DBC=∠ABC
  2 
     1     ---②
 ∠DCB=∠ACB
  2 
二等辺三角形の２つの底角は等しいので
    ∠ABC＝∠ACB    ---③

①②③より
    ∠DBC＝∠DCB

２つの角が等しい三角形は二等辺三角形であるから
    DB＝DC