証明
定期試験対策テスト 時間 50分 1/7 ページ
点
1
次の問に答えなさい． [2A1-00]
1
2点×4
△ABCと△DEFは合同である．対応する角または辺について答えなさい．
1. ∠Aの大きさ 2. ∠Fの大きさ 3. ∠Bの大きさ 4. EF＝7cmのとき，BCの大きさ | A B 50° C 70° D 60° E F |
| 1 | |
| 2 | |
| 3 | |
| 4 |
2
下図の三角形の中から合同な三角形の組を選び，記号≡を使って表しなさい．また，合同条件を書きなさい． [2B1-00]
2
順不同 完答 5点×3
7cm 65° A 6cm B C | 7cm 65° D 6cm E F | 7cm G 4cm H 4cm I |
7cm J 4cm K 4cm L | 7cm 55° M N 60° O | 7cm 55° P Q 60° R |
| (1) | |
| (2) | |
| (3) |
@2020 http://sugaku.club/
証明
定期試験対策テスト 2/7 ページ
3
次のことがらについて，仮定と結論を答えなさい． [2C0-00]
3
完答 2点×3
(1) △ABCについて ∠A＋∠B＝90°ならば ∠C＝90°である．
(2) △ABCについて ∠A＝a，∠B＝b ならば ∠c＝180-a-c である．
(3) △ABCについて ∠A＝a，∠B＝b ならば ∠c＝180-a-c である．
| (1) | 仮定 結論 |
| (2) | 仮定 結論 |
| (3) | 仮定 結論 |
4
次の問に答えなさい． [2C1-91]
4
3点×3
次の図で，AO＝CO，BO＝DOならば，△ABO≡△CDOであることを証明しなさい．
△ABOと△CDOにおいて
仮定より，
AO＝CO ---①
---②
は等しいから
∠AOB＝∠COD ---③
① ② ③ から， ので
△ABO≡△CDO
A
B
C
D
O
仮定より，
AO＝CO ---①
---②
は等しいから
∠AOB＝∠COD ---③
① ② ③ から， ので
△ABO≡△CDO
| (1) | 空欄に記入 |
@2020 http://sugaku.club/
証明
定期試験対策テスト 3/7 ページ
5
次の問に答えなさい． [2C2-91]
5
3点×4
次の図で，AO＝DO，BO＝COならば，∠B＝∠Cであることを証明しなさい．
△ABOと△DCOにおいて
仮定より，
AO＝DO ---①
---②
は等しいから
∠AOB＝∠DOC ---③
① ② ③ から， ので
△ABO≡△DCO
合同な図形では 対応する角の大きさは等しいので
A
B
C
D
O
△ABOと△DCOにおいて
仮定より，
AO＝DO ---①
---②
は等しいから
∠AOB＝∠DOC ---③
① ② ③ から， ので
△ABO≡△DCO
合同な図形では 対応する角の大きさは等しいので
| 空欄に記入 |
@2020 http://sugaku.club/
証明
定期試験対策テスト 4/7 ページ
6
次の問に答えなさい． [2C2-90]
6
12点 部分点可
次の図で，AB＝CD，AD＝CBならば，∠BCA＝∠DACであることを証明しなさい．
A
B
C
D
| 余白に記入 |
@2020 http://sugaku.club/
証明
定期試験対策テスト 5/7 ページ
7
次の問に答えなさい． [2C3-90]
7
12点 部分点可
次の図で，AB//DC，AO＝COならば，BO＝DOであることを証明しなさい．
A
B
C
D
O
| 余白に記入 |
@2020 http://sugaku.club/
証明
定期試験対策テスト 6/7 ページ
8
次の問に答えなさい． [2C3-90]
8
13点 部分点可
次の図で，AC＝AD，DB＝CEならば，BC＝DEであることを証明しなさい．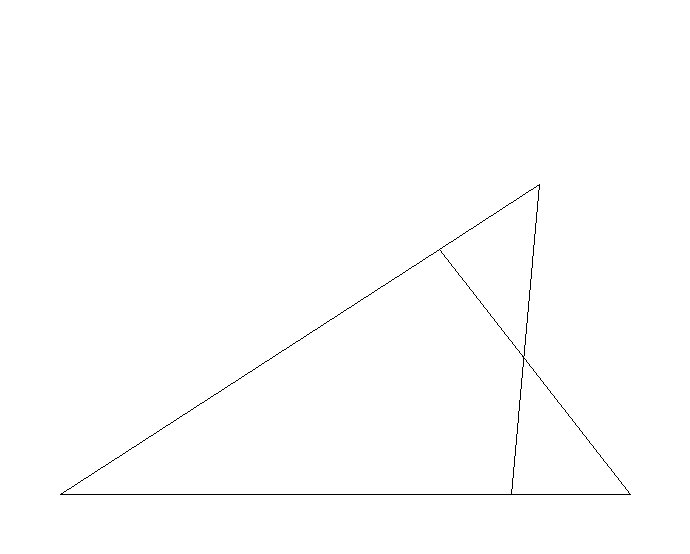
B
C
A
D
E
| 余白に記入 |
@2020 http://sugaku.club/
@2020 http://sugaku.club/
【解答例】
定期試験対策テスト 時間 50分 1/7 ページ
1
次の問に答えなさい． [2A1-00]
1
2点×4
△ABCと△DEFは合同である．対応する角または辺について答えなさい．
1. ∠Aの大きさ 2. ∠Fの大きさ 3. ∠Bの大きさ 4. EF＝7cmのとき，BCの大きさ | A B 50° C 70° D 60° E F |
| 1 | ∠A＝70° |
| 2 | ∠F＝50° |
| 3 | ∠B＝60° |
| 4 | BC＝7cm |
2
下図の三角形の中から合同な三角形の組を選び，記号≡を使って表しなさい．また，合同条件を書きなさい． [2B1-00]
2
順不同 完答 5点×3
7cm 65° A 6cm B C | 7cm 65° D 6cm E F | 7cm G 4cm H 4cm I |
7cm J 4cm K 4cm L | 7cm 55° M N 60° O | 7cm 55° P Q 60° R |
| (1) | △GHI≡△JKL ３組の辺がそれぞれ等しい |
| (2) | △ABC≡△DEF ２組の辺とその間の角がそれぞれ等しい |
| (3) | △MNO≡△PQR １組の辺とその両端の角がそれぞれ等しい． |
@2020 http://sugaku.club/
【解答例】
定期試験対策テスト 2/7 ページ
3
次のことがらについて，仮定と結論を答えなさい． [2C0-00]
3
完答 2点×3
(1) △ABCについて ∠A＋∠B＝90°ならば ∠C＝90°である．
(2) △ABCについて ∠A＝a，∠B＝b ならば ∠c＝180-a-c である．
(3) △ABCについて ∠A＝a，∠B＝b ならば ∠c＝180-a-c である．
| (1) | 仮定 ∠A＋∠B＝90° 結論 ∠C＝90° |
| (2) | 仮定 ∠A＝a，∠B＝b 結論 ∠c＝180-a-c |
| (3) | 仮定 ∠A＝a，∠B＝b 結論 ∠c＝180-a-c |
4
次の問に答えなさい． [2C1-91]
4
3点×3
次の図で，AO＝CO，BO＝DOならば，△ABO≡△CDOであることを証明しなさい．△ABOと△CDOにおいて
仮定より，
AO＝CO ---①
BO ＝ DO ---②
対頂角 は等しいから
∠AOB＝∠COD ---③
① ② ③ から， ２組の辺とその間の角がそれぞれ等しい ので
△ABO≡△CDO
A
B
C
D
O
仮定より，
AO＝CO ---①
BO ＝ DO ---②
対頂角 は等しいから
∠AOB＝∠COD ---③
① ② ③ から， ２組の辺とその間の角がそれぞれ等しい ので
△ABO≡△CDO
| (1) | 空欄に記入 |
@2020 http://sugaku.club/
【解答例】
定期試験対策テスト 3/7 ページ
5
次の問に答えなさい． [2C2-91]
5
3点×4
次の図で，AO＝DO，BO＝COならば，∠B＝∠Cであることを証明しなさい．
△ABOと△DCOにおいて
仮定より，
AO＝DO ---①
BO ＝ CO ---②
対頂角 は等しいから
∠AOB＝∠DOC ---③
① ② ③ から， ２組の辺とその間の角がそれぞれ等しい ので
△ABO≡△DCO
合同な図形では 対応する角の大きさは等しいので
∠B ＝ ∠C
A
B
C
D
O
△ABOと△DCOにおいて
仮定より，
AO＝DO ---①
BO ＝ CO ---②
対頂角 は等しいから
∠AOB＝∠DOC ---③
① ② ③ から， ２組の辺とその間の角がそれぞれ等しい ので
△ABO≡△DCO
合同な図形では 対応する角の大きさは等しいので
∠B ＝ ∠C
| 空欄に記入 |
@2020 http://sugaku.club/
【解答例】
定期試験対策テスト 4/7 ページ
6
次の問に答えなさい． [2C2-90]
6
12点 部分点可
次の図で，AB＝CD，AD＝CBならば，∠BCA＝∠DACであることを証明しなさい．
△ABCと△CDAにおいて
仮定より，
AB＝CD ---①
AD＝CB ---②
また，ACは共通だから
AC＝AC ---③
① ② ③ から，３組の辺がそれぞれ等しい ので
△ABC≡△ADC
合同な図形では 対応する角の大きさは等しいので
∠BCA＝∠DAC
A
B
C
D
△ABCと△CDAにおいて
仮定より，
AB＝CD ---①
AD＝CB ---②
また，ACは共通だから
AC＝AC ---③
① ② ③ から，３組の辺がそれぞれ等しい ので
△ABC≡△ADC
合同な図形では 対応する角の大きさは等しいので
∠BCA＝∠DAC
| 余白に記入 |
@2020 http://sugaku.club/
【解答例】
定期試験対策テスト 5/7 ページ
7
次の問に答えなさい． [2C3-90]
7
12点 部分点可
次の図で，AB//DC，AO＝COならば，BO＝DOであることを証明しなさい．
△ABOと△CDOにおいて
仮定より，
AO＝CO ---①
AB//DCより，錯角は等しいから
∠BAO＝∠DCO ---②
対頂角は等しいから
∠AOB＝∠COD ---③
① ② ③ から，１組の辺とその両端の角がそれぞれ等しい ので
△ABO≡△CDO
合同な図形では 対応する辺の大きさは等しいので
BO＝DO
A
B
C
D
O
△ABOと△CDOにおいて
仮定より，
AO＝CO ---①
AB//DCより，錯角は等しいから
∠BAO＝∠DCO ---②
対頂角は等しいから
∠AOB＝∠COD ---③
① ② ③ から，１組の辺とその両端の角がそれぞれ等しい ので
△ABO≡△CDO
合同な図形では 対応する辺の大きさは等しいので
BO＝DO
| 余白に記入 |
@2020 http://sugaku.club/
【解答例】
定期試験対策テスト 6/7 ページ
8
次の問に答えなさい． [2C3-90]
8
13点 部分点可
次の図で，AC＝AD，DB＝CEならば，BC＝DEであることを証明しなさい．
△ABCと△AEDにおいて，
仮定より，
AC＝AD ---①
DB＝CE ---②
また，
AB＝AD＋DB ---③
AE＝AC＋CE ---④
① ② ③ ④ から，
AB＝AE ---⑤
また， ∠A は共通 ---⑥
① ⑤ ⑥ から， ２組の辺とその間の角がそれぞれ等しい ので
△ABC≡△AED
合同な図形では 対応する辺の大きさは等しいので
BC＝DE
B
C
A
D
E
△ABCと△AEDにおいて，
仮定より，
AC＝AD ---①
DB＝CE ---②
また，
AB＝AD＋DB ---③
AE＝AC＋CE ---④
① ② ③ ④ から，
AB＝AE ---⑤
また， ∠A は共通 ---⑥
① ⑤ ⑥ から， ２組の辺とその間の角がそれぞれ等しい ので
△ABC≡△AED
合同な図形では 対応する辺の大きさは等しいので
BC＝DE
| 余白に記入 |
@2020 http://sugaku.club/
【解答例】
定期試験対策テスト 7/7 ページ
9
次の問に答えなさい． [2C3-90]
9
13点 部分点可
次の図で，∠A＋∠B＝∠C＋∠D となることを証明しなさい．
△ABOと△DCOにおいて，三角形の内角の和は180°だから，
∠A＋∠B＋∠AOB＝180° ---①
∠C＋∠D＋∠DOC＝180° ---②
① ② から，
∠A＋∠B＋∠AOB＝∠C＋∠D＋∠DOC ---③
また，対頂角は等しいので
∠AOB＝∠DOC ---④
③ ④ から，
∠A＋∠B＝∠C＋∠D
A
B
C
D
O
△ABOと△DCOにおいて，三角形の内角の和は180°だから，
∠A＋∠B＋∠AOB＝180° ---①
∠C＋∠D＋∠DOC＝180° ---②
① ② から，
∠A＋∠B＋∠AOB＝∠C＋∠D＋∠DOC ---③
また，対頂角は等しいので
∠AOB＝∠DOC ---④
③ ④ から，
∠A＋∠B＝∠C＋∠D
| 余白に記入 |
@2020 http://sugaku.club/