確率
定期試験対策テスト 時間 50分 1/8 ページ
点
1
次の問に答えなさい. [2Q0-01]
1
完答 7点
サイコロを何回か投げた時,偶数または奇数の目が出た回数を記録しました.偶数の目が出る確率 を求めなさい.また,サイコロを何回か投げた時,偶数または奇数の目が出た回数を記録しました. 表の空欄に値を小数第3位を四捨五入して書きなさい.
| 回数 | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
| 奇数 | 6 | 8 | 25 | 55 | 99 | 244 | 492 |
| 偶数 | 4 | 12 | 25 | 45 | 101 | 256 | 508 |
| 偶数の相対度数 | 0.55 | 0.50 | 0.49 | 0.49 |
| 1 |
2
次の問に答えなさい. [2Q1-00]
2
3点×2
(1) 硬貨をくり返し300回投げた時,表が出た回数を調べたところ146回でした.表が出る確率を小数第2位まで求めなさい.
(2) ある都市の過去100年間の天気の記録から,10月10日に晴天であった日数を調べると79日でした.この都市の10月10日の晴天の確率を小数第2位まで求めなさい.
| (1) | |
| (2) |
3
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい. [2R2-01]
3
完答 7点
(1) A,B,Cの3枚のカードから1枚ずつ3枚引く時,カードの順番は何通りあるか樹形図を使って求めなさい.また,樹形図の空欄を埋めなさい.
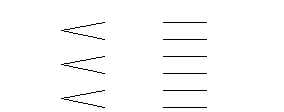
1回目
2回目
3回目
A
C
B
A
C
A
B
C
B
C
A
B
A
| (1) | 通り |
@2026 http://sugaku.club/
確率
定期試験対策テスト 2/8 ページ
4
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい. [2R0-00]
4
完答 10点
(1) 赤,白,黄の3色の玉が1個ずつ入っている袋があります.その袋から1個ずつ3個の玉を取り出す時,赤,白,黄の順に取り出す確率を樹形図を使って求めなさい.樹形図は余白に記入すること.
| (1) |
5
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
5
4点×3
(1) 赤玉2個,白玉3個,黄玉1個,青玉2個が入っている袋があります.その袋から1個を選ぶ時,何通りの選び方がありますか. [2T0-00]
(2) 1,2,3,4,5の5枚のカードをから1枚を選ぶ時,3未満の数のカードを選ぶ確率を求めなさい. [2T4-00]
(3) Aのカードが4枚,Bのカードが1枚,Cのカードが2枚あります.この中から1枚を選ぶ時,Bのカードを選ぶ確率を求めなさい. [2T4-00]
| (1) | 通り |
| (2) | |
| (3) |
@2026 http://sugaku.club/
確率
定期試験対策テスト 3/8 ページ
6
次の問に答えなさい.
6
4点×2
(1) A,B,Cの3枚のカードを並べるとき,何通りの並べ方がありますか. [2S0-00]
(2) A,B,Cの3枚のカードを左から右に並べるとき,Aが左端に並ぶ場合は何通りありますか. [2S1-00]
| (1) | 通り |
| (2) | 通り |
@2026 http://sugaku.club/
確率
定期試験対策テスト 4/8 ページ
7
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
7
5点×2
(1) 0,1,2,3の4枚のカードから2枚を選び左から右に並べて整数をつくる時,2けたの整数になる確率を求めなさい. [2S2-00]
(2) A,B,Cの3枚のカードをから 1枚ずつ 2枚を取り出す時,カードの選び方は何通りありますか. [2T1-00]
| (1) | |
| (2) | 通り |
@2026 http://sugaku.club/
確率
定期試験対策テスト 5/8 ページ
8
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
8
5点×2
(1) 赤玉2個,白玉4個が入っている袋があります.その袋から2個を選ぶ時,何通りの選び方がありますか. [2T2-00]
(2) 1,2,3,4の4枚のカードをから 1枚ずつ 2枚を取り出す時,数の和が6以上になる確率を求めなさい. [2T5-00]
| (1) | 通り |
| (2) |
@2026 http://sugaku.club/
確率
定期試験対策テスト 6/8 ページ
9
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
9
5点×2
(1) Aのカードが1枚,Bのカードが5枚があります.この中から2枚を選ぶ時,Bのカード2枚が選ばれる確率を求めなさい. [2T6-00]
(2) 2枚のコインを同時に投げる時,2枚とも裏になる確率を求めなさい. [2U0-00]
| (1) | |
| (2) |
@2026 http://sugaku.club/
確率
定期試験対策テスト 7/8 ページ
10
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
10
5点×2
(1) あたりが1本,はずれが5本が入っているくじがあります.このくじを同時に2本ひくとき,少なくとも1本があたりである確率を求めなさい. [2U1-00]
(2) 男子2人,女子4人からくじによって2人役員を選ぶ時,男子の役員2人が選ばれる確率を求めなさい. [2U1-00]
| (1) | |
| (2) |
@2026 http://sugaku.club/
確率
定期試験対策テスト 8/8 ページ
11
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
11
5点×2
(1) 大小2個のさいころを同時にふる時,出た目の積が12以下になる確率を求めなさい. [2U2-00]
| (1) | |
| (2) |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 時間 50分 1/8 ページ
1
次の問に答えなさい. [2Q0-01]
1
完答 7点
サイコロを何回か投げた時,偶数または奇数の目が出た回数を記録しました.偶数の目が出る確率 を求めなさい.また,サイコロを何回か投げた時,偶数または奇数の目が出た回数を記録しました. 表の空欄に値を小数第3位を四捨五入して書きなさい.
| 回数 | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
| 奇数 | 6 | 8 | 25 | 55 | 99 | 244 | 492 |
| 偶数 | 4 | 12 | 25 | 45 | 101 | 256 | 508 |
| 偶数の相対度数 | 0.60 | 0.40 | 0.50 | 0.55 | 0.50 | 0.49 | 0.49 |
| 1 | およそ0.49 |
2
次の問に答えなさい. [2Q1-00]
2
3点×2
(1) 硬貨をくり返し300回投げた時,表が出た回数を調べたところ146回でした.表が出る確率を小数第2位まで求めなさい.
| ≒0.49 | |||||
| ||||||
(2) ある都市の過去100年間の天気の記録から,10月10日に晴天であった日数を調べると79日でした.この都市の10月10日の晴天の確率を小数第2位まで求めなさい.
| =0.79 | |||||
| ||||||
| (1) | およそ0.49 |
| (2) | およそ0.79 |
3
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい. [2R2-01]
3
完答 7点
(1) A,B,Cの3枚のカードから1枚ずつ3枚引く時,カードの順番は何通りあるか樹形図を使って求めなさい.また,樹形図の空欄を埋めなさい.

1回目
2回目
3回目
A
B
C
B
C
A
C
A
B
C
B
C
A
B
A
| (1) | 6通り |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 2/8 ページ
4
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい. [2R0-00]
4
完答 10点
(1) 赤,白,黄の3色の玉が1個ずつ入っている袋があります.その袋から1個ずつ3個の玉を取り出す時,赤,白,黄の順に取り出す確率を樹形図を使って求めなさい.樹形図は余白に記入すること.
 上の樹形図は起こるすべての場合を示していて,全部で6通りの出かたがあることがわかります.このうち,赤,白,黄の順に取り出す出かたは,1通りです.
上の樹形図は起こるすべての場合を示していて,全部で6通りの出かたがあることがわかります.このうち,赤,白,黄の順に取り出す出かたは,1通りです.
1回目
2回目
3回目
赤
白
黄
白
黄
赤
黄
赤
白
黄 ◯
白
黄
赤
白
赤
| (1) |
|
5
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
5
4点×3
(1) 赤玉2個,白玉3個,黄玉1個,青玉2個が入っている袋があります.その袋から1個を選ぶ時,何通りの選び方がありますか. [2T0-00]
赤が2通り 白が3通り 黄が1通り 青が2通り で,合計8通りの選び方がある
赤が2通り 白が3通り 黄が1通り 青が2通り で,合計8通りの選び方がある
(2) 1,2,3,4,5の5枚のカードをから1枚を選ぶ時,3未満の数のカードを選ぶ確率を求めなさい. [2T4-00]
起こりうるすべての場合の数は,1,2,3,4,5の5通り.
3未満の数のカードは,1,2の2通り.
起こりうるすべての場合の数は,1,2,3,4,5の5通り.
3未満の数のカードは,1,2の2通り.
| なので,確率は | 2 | ||
| 5 | |||
(3) Aのカードが4枚,Bのカードが1枚,Cのカードが2枚あります.この中から1枚を選ぶ時,Bのカードを選ぶ確率を求めなさい. [2T4-00]
起こりうるすべての場合の数は,Aのカードが4通り Bのカードが1通り Cのカードが2通り で,合計7通りの選び方がある.
Bのカードを選ぶ場合の数は,1通り.
起こりうるすべての場合の数は,Aのカードが4通り Bのカードが1通り Cのカードが2通り で,合計7通りの選び方がある.
Bのカードを選ぶ場合の数は,1通り.
| なので,確率は | 1 | ||
| 7 | |||
| (1) | 8通り | ||||||||
| (2) |
|
||||||||
| (3) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 3/8 ページ
6
次の問に答えなさい.
6
4点×2
(1) A,B,Cの3枚のカードを並べるとき,何通りの並べ方がありますか. [2S0-00]
[樹形図で求める方法] [計算で求める方法]
[計算で求める方法]
最も左はABCの3通り,真ん中は左以外のカードで2通り,最も右は残る1通りなので,
3×2×1=6
[樹形図で求める方法]
A
B
C
B
C
A
C
A
B
C
B
C
A
B
A
最も左はABCの3通り,真ん中は左以外のカードで2通り,最も右は残る1通りなので,
3×2×1=6
(2) A,B,Cの3枚のカードを左から右に並べるとき,Aが左端に並ぶ場合は何通りありますか. [2S1-00]
[樹形図で求める方法]
 [計算で求める方法]
[計算で求める方法]
左端はAの1通り,中はA以外の2通り,右端は残る1通りなので,
1×2×1=2
[樹形図で求める方法]
左
中
右
A
B
C
B
C
A
C
A
B
C ◯
B ◯
C
A
B
A
左端はAの1通り,中はA以外の2通り,右端は残る1通りなので,
1×2×1=2
| (1) | 6通り |
| (2) | 2通り |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 4/8 ページ
7
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
7
5点×2
(1) 0,1,2,3の4枚のカードから2枚を選び左から右に並べて整数をつくる時,2けたの整数になる確率を求めなさい. [2S2-00]
[樹形図で求める方法]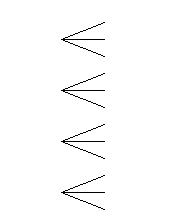 [計算で求める方法]
[計算で求める方法]
4枚のカードから2枚を選び並べる場合,全部で12通り.(4×3=12). 2けたの整数になるには,十の位の数が1,2,3の場合.よって,十の位は1,2,3の3通り,一の位は十の位以外の3通りなので,3×3=9 通り
[樹形図で求める方法]
十
一
0
1
2
3
1
2
3
0 ◯
2 ◯
3 ◯
0 ◯
1 ◯
3 ◯
0 ◯
1 ◯
2 ◯
4枚のカードから2枚を選び並べる場合,全部で12通り.(4×3=12). 2けたの整数になるには,十の位の数が1,2,3の場合.よって,十の位は1,2,3の3通り,一の位は十の位以外の3通りなので,3×3=9 通り
| 確率は |
| 3 | ||||||
| = | ||||||||
| 4 | |||||||
| (1) |
|
||||||||
| (2) | 3通り |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 5/8 ページ
8
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
8
5点×2
(1) 赤玉2個,白玉4個が入っている袋があります.その袋から2個を選ぶ時,何通りの選び方がありますか. [2T2-00]
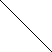 | 赤1 | 赤2 | 白1 | 白2 | 白3 | 白4 |
| 赤1 |  | ◯ | ◯ | ◯ | ◯ | ◯ |
| 赤2 |  | ◯ | ◯ | ◯ | ◯ | |
| 白1 |  | ◯ | ◯ | ◯ | ||
| 白2 |  | ◯ | ◯ | |||
| 白3 |  | ◯ | ||||
| 白4 |  |
(2) 1,2,3,4の4枚のカードをから 1枚ずつ 2枚を取り出す時,数の和が6以上になる確率を求めなさい. [2T5-00]
4枚のカードから2枚を選ぶすべての組み合わせは,6通り
2枚の和が6以上になるカードは,24,34の2通り.
 | 1 | 2 | 3 | 4 |
| 1 |  | |||
| 2 |  |  | ◯ | |
| 3 |  |  |  | ◯ |
| 4 |  |  |  |  |
4枚のカードから2枚を選ぶすべての組み合わせは,6通り
2枚の和が6以上になるカードは,24,34の2通り.
| なので,確率は |
| 1 | ||||||
| = | ||||||||
| 3 | |||||||
| (1) | 15通り | ||||||||
| (2) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 6/8 ページ
9
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
9
5点×2
(1) Aのカードが1枚,Bのカードが5枚があります.この中から2枚を選ぶ時,Bのカード2枚が選ばれる確率を求めなさい. [2T6-00]
6枚のカードから2枚を選ぶ場合,全部で15通り.
Bのカード2枚が選ばれる場合の数は,10通り.(B1B2 , B1B3 , B1B4 , B1B5 , B2B3 , B2B4 , B2B5 , B3B4 , B3B5 , B4B5)
 | A | B1 | B2 | B3 | B4 | B5 |
| A |  | |||||
| B1 |  |  | ◯ | ◯ | ◯ | ◯ |
| B2 |  |  |  | ◯ | ◯ | ◯ |
| B3 |  |  |  |  | ◯ | ◯ |
| B4 |  |  |  |  |  | ◯ |
| B5 |  |  |  |  |  |  |
Bのカード2枚が選ばれる場合の数は,10通り.(B1B2 , B1B3 , B1B4 , B1B5 , B2B3 , B2B4 , B2B5 , B3B4 , B3B5 , B4B5)
| なので,確率は |
| 2 | ||||||
| = | ||||||||
| 3 | |||||||
(2) 2枚のコインを同時に投げる時,2枚とも裏になる確率を求めなさい. [2U0-00]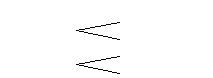 2枚のコインを区別すると,表裏の出かたは4通り.
2枚のコインを区別すると,表裏の出かたは4通り.
2枚とも裏になる場合は,1通り
コインA
コインB
表
裏
表
裏
表
裏 ◯
2枚とも裏になる場合は,1通り
| 確率は | 1 | ||
| 4 | |||
| (1) |
|
||||||||
| (2) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 7/8 ページ
10
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
10
5点×2
(1) あたりが1本,はずれが5本が入っているくじがあります.このくじを同時に2本ひくとき,少なくとも1本があたりである確率を求めなさい. [2U1-00]
6本のくじから2本を同時にひく場合,全部で15通り.
少なくとも1本があたりである場合の数は,5通り.
 | 当 | は1 | は2 | は3 | は4 | は5 |
| 当 |  | ◯ | ◯ | ◯ | ◯ | ◯ |
| は1 |  |  | ||||
| は2 |  |  |  | |||
| は3 |  |  |  |  | ||
| は4 |  |  |  |  |  | |
| は5 |  |  |  |  |  |  |
少なくとも1本があたりである場合の数は,5通り.
| なので,確率は |
| 1 | ||||||
| = | ||||||||
| 3 | |||||||
(2) 男子2人,女子4人からくじによって2人役員を選ぶ時,男子の役員2人が選ばれる確率を求めなさい. [2U1-00]
6人から2人を選ぶ場合,全部で15通り
男子の役員2人が選ばれる場合の数は,1通り.
 | 男1 | 男2 | 女1 | 女2 | 女3 | 女4 |
| 男1 |  | ◯ | ||||
| 男2 |  |  | ||||
| 女1 |  |  |  | |||
| 女2 |  |  |  |  | ||
| 女3 |  |  |  |  |  | |
| 女4 |  |  |  |  |  |  |
男子の役員2人が選ばれる場合の数は,1通り.
| なので,確率は | 1 | ||
| 15 | |||
| (1) |
|
||||||||
| (2) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 8/8 ページ
11
起こりうるすべての場合が,同様に確からしいとして次の問に答えなさい.
11
5点×2
(1) 大小2個のさいころを同時にふる時,出た目の積が12以下になる確率を求めなさい. [2U2-00]
2個のさいころを同時にふった時,全部で36通りの場合がある.(6×6=36)
出た目の積が12以下になる場合は,23通り.
| 大 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 小 | 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | |
出た目の積が12以下になる場合は,23通り.
| 確率は | 23 | ||
| 36 | |||
(2) 太郎くんと次郎くんがじゃんけんをした時,次郎くんが負けない確率を求めなさい. [2U3-00]
二人でじゃんけんをした時,全部で9通りの場合がある.(3×3=9)
次郎くんが負けない場合は,6通り.
| 太郎 | ||||
| グー | チョキ | パー | ||
| 次郎 | グー |  |  | |
| チョキ |  |  | ||
| パー |  |  | ||
次郎くんが負けない場合は,6通り.
| 確率は |
| 2 | ||||||
| = | ||||||||
| 3 | |||||||
| (1) |
|
||||||||
| (2) |
|
@2026 http://sugaku.club/