式の計算
定期試験対策テスト 時間 50分 1/6 ページ
点
1
次の計算をしなさい
1
2点×9
| (1) | [140-00] | |||||||||
| 2 | x | − | 8 | x | − | 9 | y | |||
| (2) | [140-10] | |||||||||
| 0.4 | x | − | 0.9 | x | + | 0.4 | y | |||
| (3) | [144-00] | |||||||
| 9 | ( | x | − | y | ) | |||
| (4) | 1 | 1 | 1 | 4 | [144-20] | |||||||
| ( | a | + | b | − | ) | |||||||
| 2 | 6 | 2 | 5 | |||||||||
| (5) | [141-00] | ||||||||||||||
| 10 | x | y | + | 3 | x | + | 8 | y | z | − | 5 | x | |||
| (6) | [142-00] | ||||||||||||||||||||
| ( | 6 | a | + | 2 | b | − | 1 | ) | − | ( | 8 | a | + | 6 | b | + | 3 | ) | |||
| (7) |
|
| [143-00] | ||||||||||||||||||||||||
| ( | 5 | u | + | 10 | u | − | 9 | ) | + | ( | 4 | u | − | 4 | u | ) | |||||||||||
| (8) | [145-00] | ||||||||||||||||
| 6 | ( | 10 | x | + | 2 | ) | − | 2 | ( | 10 | x | + | 4 | ) | |||
| (9) | 3 | 3 | 1 | 3 | 1 | 3 | 3 | 4 | [145-20] | ||||||||||||||
| ( | p | + | q | − | ) | + | ( | p | + | q | + | ) | |||||||||||
| 4 | 4 | 3 | 7 | 2 | 4 | 4 | 5 | ||||||||||||||||
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| (5) | |
| (6) | |
| (7) | |
| (8) | |
| (9) |
@2026 http://sugaku.club/
式の計算
定期試験対策テスト 2/6 ページ
2
次の計算をしなさい
2
2点×2
(1) [150-00]
| − |
| ||||||||||||||||||||||||||
| +) |
| + |
|
(2) [151-00]
| − |
| |||||||||||||||||||||||||||||
| +) |
| − |
|
| (1) | |
| (2) |
3
次の計算をしなさい
3
2点×9
| (1) | [160-00] | ||||||||
| −2 | u | × | ( | −7 | ) | w | |||
| (2) | 1 | 5 | [160-20] | ||||
| u | × | u | |||||
| 4 | 6 | ||||||
| (3) |
|
| [161-00] | ||||||||||||
| 4 | a | × | 7 | a | |||||||||||
| (4) | 1 |
| 2 |
| [161-20] | ||||||||||||||
| u | v | × | ( | − | ) | v | |||||||||||||
| 2 | 3 | ||||||||||||||||||
| (5) |
|
| [162-00] | |||||||||||||||
| 25 | q | ÷ | ( | −5 | p | q | ) | |||||||||||
| (6) | 1 |
| 2 |
|
| [162-20] | ||||||||||||||||
| u | ÷ | ( | u | v | ) | |||||||||||||||||
| 2 | 3 | |||||||||||||||||||||
| (7) |
|
|
|
| [163-00] | |||||||||||||||||||||||||
| −5 | q | r | × | ( | −3 | ) | q | × | 6 | p | q | |||||||||||||||||||
| (8) |
|
|
| [163-00] | |||||||||||||||||||||||
| −8 | y | z | ÷ | ( | −8 | x | ) | ÷ | ( | 10 | y | ) | |||||||||||||||
| (9) | 3 | 1 |
| 1 |
| [163-20] | |||||||||||||||||
| a | × | b | c | × | ( | − | ) | b | c | ||||||||||||||
| 5 | 5 | 3 | |||||||||||||||||||||
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| (5) | |
| (6) | |
| (7) | |
| (8) | |
| (9) |
@2026 http://sugaku.club/
式の計算
定期試験対策テスト 3/6 ページ
4
次の問に答えなさい
4
3点×4
| (1) | |
| (2) | |
| (3) | |
| (4) |
@2026 http://sugaku.club/
式の計算
定期試験対策テスト 4/6 ページ
5
次の等式を[ ]内の変数について解きなさい
5
4点×6
| (1) | [w] [180-00] | ||||||||
| 4 | v | + | 10 | w | = | 4 | |||
| (2) | 1 | 4 | [r] [180-20] | |||||||
| − | q | − | r | = | 0 | |||||
| 4 | 5 | |||||||||
| (3) | [v] [181-00] | |||||
| u | = | 4 | v | |||
| (4) | 4 | [b] [181-20] | |||||
| a | = | − | b | ||||
| 5 | |||||||
| (5) |
| [b] [182-00] | ||||||||||||
| a | = | |||||||||||||
| ||||||||||||||
| (6) | 5 | [b] [182-20] | |||||||||||
| X | = | − | ( | a | + | b | + | c | ) | ||||
| 3 | |||||||||||||
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| (5) | |
| (6) |
@2026 http://sugaku.club/
式の計算
定期試験対策テスト 5/6 ページ
6
次の問に答えなさい
6
5点×3
| (1) | |
| (2) | |
| (3) |
@2026 http://sugaku.club/
式の計算
定期試験対策テスト 6/6 ページ
7
次の問に答えなさい
7
9点
| (1) | 余白に記入 |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 時間 50分 1/6 ページ
1
次の計算をしなさい
1
2点×9
| (1) | [140-00] | |||||||||
| 2 | x | − | 8 | x | − | 9 | y | |||
| (2) | [140-10] | |||||||||
| 0.4 | x | − | 0.9 | x | + | 0.4 | y | |||
| (3) | [144-00] | |||||||
| 9 | ( | x | − | y | ) | |||
| (4) | 1 | 1 | 1 | 4 | [144-20] | |||||||
| ( | a | + | b | − | ) | |||||||
| 2 | 6 | 2 | 5 | |||||||||
| (5) | [141-00] | ||||||||||||||
| 10 | x | y | + | 3 | x | + | 8 | y | z | − | 5 | x | |||
| (6) | [142-00] | ||||||||||||||||||||
| ( | 6 | a | + | 2 | b | − | 1 | ) | − | ( | 8 | a | + | 6 | b | + | 3 | ) | |||
| (7) |
|
| [143-00] | ||||||||||||||||||||||||
| ( | 5 | u | + | 10 | u | − | 9 | ) | + | ( | 4 | u | − | 4 | u | ) | |||||||||||
| (8) | [145-00] | ||||||||||||||||
| 6 | ( | 10 | x | + | 2 | ) | − | 2 | ( | 10 | x | + | 4 | ) | |||
| = | 6 | × | 10 | x | + | 6 | × | 2 | − | 2 | × | 10 | x | − | 2 | × | 4 | = | 40 | x | + | 4 | |||
| (9) | 3 | 3 | 1 | 3 | 1 | 3 | 3 | 4 | [145-20] | ||||||||||||||
| ( | p | + | q | − | ) | + | ( | p | + | q | + | ) | |||||||||||
| 4 | 4 | 3 | 7 | 2 | 4 | 4 | 5 | ||||||||||||||||
| 3 | 3 | 3 | 1 | 3 | 3 | 1 | 3 | 1 | 3 | 1 | 4 | 15 | 5 | 11 | ||||||||||||||||||||||||
| = | × | p | + | × | q | − | × | + | × | p | + | × | q | + | × | = | p | + | q | + | ||||||||||||||||||
| 4 | 4 | 4 | 3 | 4 | 7 | 2 | 4 | 2 | 4 | 2 | 5 | 16 | 8 | 140 | ||||||||||||||||||||||||
| (1) |
|
||||||||||||||||||||||||||||||||||||
| (2) |
|
||||||||||||||||||||||||||||||||||||
| (3) |
|
||||||||||||||||||||||||||||||||||||
| (4) |
|
||||||||||||||||||||||||||||||||||||
| (5) |
|
||||||||||||||||||||||||||||||||||||
| (6) |
|
||||||||||||||||||||||||||||||||||||
| (7) |
|
||||||||||||||||||||||||||||||||||||
| (8) |
|
||||||||||||||||||||||||||||||||||||
| (9) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 2/6 ページ
2
次の計算をしなさい
2
2点×2
(1) [150-00]
| − |
| ||||||||||||||||||||||||||
| +) |
| + |
|
(2) [151-00]
| − |
| |||||||||||||||||||||||||||||
| +) |
| − |
|
| (1) |
|
||||||||||||||||||||||||
| (2) |
|
3
次の計算をしなさい
3
2点×9
| (1) | [160-00] | ||||||||
| −2 | u | × | ( | −7 | ) | w | |||
| = | 14 | u | w | |||
| (2) | 1 | 5 | [160-20] | ||||
| u | × | u | |||||
| 4 | 6 | ||||||
| 5 |
| ||||||||
| = | u | ||||||||
| 24 | |||||||||
| (3) |
|
| [161-00] | ||||||||||||
| 4 | a | × | 7 | a | |||||||||||
|
|
| |||||||||||||||||||||
| = | 4 | a | × | 7 | a | = | 28 | a | |||||||||||||||
| (4) | 1 |
| 2 |
| [161-20] | ||||||||||||||
| u | v | × | ( | − | ) | v | |||||||||||||
| 2 | 3 | ||||||||||||||||||
| 1 |
| 2 |
| 1 |
| ||||||||||||||||||||||||
| = | u | v | × | ( | − | ) | v | = | − | u | v | ||||||||||||||||||
| 2 | 3 | 3 | |||||||||||||||||||||||||||
| (5) |
|
| [162-00] | |||||||||||||||
| 25 | q | ÷ | ( | −5 | p | q | ) | |||||||||||
|
| ||||||||||||||||||||||||
| = | = | − | |||||||||||||||||||||||
|
| ||||||||||||||||||||||||
| (6) | 1 |
| 2 |
|
| [162-20] | ||||||||||||||||
| u | ÷ | ( | u | v | ) | |||||||||||||||||
| 2 | 3 | |||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||
| = | = | ||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||
| (7) |
|
|
|
| [163-00] | |||||||||||||||||||||||||
| −5 | q | r | × | ( | −3 | ) | q | × | 6 | p | q | |||||||||||||||||||
|
| ||||||||||||||
| = | 90 | p | q | r | |||||||||||
| (8) |
|
|
| [163-00] | |||||||||||||||||||||||
| −8 | y | z | ÷ | ( | −8 | x | ) | ÷ | ( | 10 | y | ) | |||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
| = | = | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
| (9) | 3 | 1 |
| 1 |
| [163-20] | |||||||||||||||||
| a | × | b | c | × | ( | − | ) | b | c | ||||||||||||||
| 5 | 5 | 3 | |||||||||||||||||||||
| 1 |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | = | − | a | b | c | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) |
|
||||||||||||||||||||||||||||||||||||||
| (2) |
|
||||||||||||||||||||||||||||||||||||||
| (3) |
|
||||||||||||||||||||||||||||||||||||||
| (4) |
|
||||||||||||||||||||||||||||||||||||||
| (5) |
|
||||||||||||||||||||||||||||||||||||||
| (6) |
|
||||||||||||||||||||||||||||||||||||||
| (7) |
|
||||||||||||||||||||||||||||||||||||||
| (8) |
|
||||||||||||||||||||||||||||||||||||||
| (9) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 3/6 ページ
4
次の問に答えなさい
4
3点×4
| (2) | 3 | 1 | のとき,次の式の値を計算しなさい. [170-20] | |||||||
| a | = | − | , | b | = | |||||
| 4 | 2 | |||||||||
| 6 | 1 | 1 | 1 | 4 | 6 | |||||||||||||||||
| − | { | − | a | − | ( | − | ) | } | − | ( | a | − | ) | |||||||||
| 5 | 5 | 4 | 3 | 5 | 5 | |||||||||||||||||
| 2 | 1 | |||||||
| = | − | a | + | |||||
| 75 | 10 | |||||||
| 2 | 3 | 1 | 3 | |||||||||||
| = | − | × | ( | − | ) | + | = | |||||||
| 75 | 4 | 10 | 25 | |||||||||||
| (3) | のとき,次の式の値を計算しなさい. [171-00] | ||||||||
| x | = | −3 | , | y | = | −2 | |||
|
|
| |||||||||||||||||||||||||
| −5 | x | ÷ | ( | 2 | x | ) | ÷ | ( | 2 | x | y | ) | |||||||||||||||
|
|
| 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | = | − | = | − | = | − | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| 1296 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) |
|
|||||||||||
| (2) |
|
|||||||||||
| (3) |
|
|||||||||||
| (4) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 4/6 ページ
5
次の等式を[ ]内の変数について解きなさい
5
4点×6
| (1) | [w] [180-00] | ||||||||
| 4 | v | + | 10 | w | = | 4 | |||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
| (2) | 1 | 4 | [r] [180-20] | |||||||
| − | q | − | r | = | 0 | |||||
| 4 | 5 | |||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
| (3) | [v] [181-00] | |||||
| u | = | 4 | v | |||
|
|
||||||||||||||||||||||||
|
|
| (4) | 4 | [b] [181-20] | |||||
| a | = | − | b | ||||
| 5 | |||||||
|
|
||||||||||||||||||||||||||
|
|
| (5) |
| [b] [182-00] | ||||||||||||
| a | = | |||||||||||||
| ||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
| (6) | 5 | [b] [182-20] | |||||||||||
| X | = | − | ( | a | + | b | + | c | ) | ||||
| 3 | |||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
| (1) |
|
||||||||||||||||||||||||||||||||
| (2) |
|
||||||||||||||||||||||||||||||||
| (3) |
|
||||||||||||||||||||||||||||||||
| (4) |
|
||||||||||||||||||||||||||||||||
| (5) |
|
||||||||||||||||||||||||||||||||
| (6) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 5/6 ページ
6
次の問に答えなさい
6
5点×3
(1) 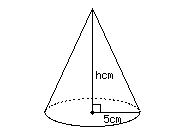 底面の半径が 5cm,高さが h cmの円錐があります.この円錐の高さを2cm大きくした時,円錐の体積は何cm3大きくなるか求めなさい. [191-00]
底面の半径が 5cm,高さが h cmの円錐があります.この円錐の高さを2cm大きくした時,円錐の体積は何cm3大きくなるか求めなさい. [191-00]
[解説]
[解説]
円錐の体積は,1/3×(底面積)×(高さ) で求められる.答えは,高さが2cm大きい円錐の体積から,もとの円錐の体積を引くことで求められる.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(2) 半径が r cmの円があります.この円の半径を8cm大きくした時,円周の長さは何cm大きくなるか求めなさい. [191-00]
[解説]
[解説]
半径 r cmの円の円周の長さは,2πr cm である.答えは,半径が8cm大きい円の円周の長さから,もとの円周の長さを引くことで求められる.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(3) 半径が r cmの円があります.この円の半径を3cm大きくした時,円周の長さは何cm大きくなるか求めなさい. [191-00]
[解説]
[解説]
半径 r cmの円の円周の長さは,2πr cm である.答えは,半径が3cm大きい円の円周の長さから,もとの円周の長さを引くことで求められる.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| (1) |
|
||||||||||||
| (2) |
|
||||||||||||
| (3) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 6/6 ページ
7
次の問に答えなさい
7
9点
(1) 十の位の数と一の位の数の異なる2けたの自然数があります.この数の十の位と一の位の数を入れかえてできる数との差が,9の倍数になることを説明しなさい. [190-00]
[解説]
[解説]
もとの数の十の位の数をa,一の位の数をbとすると,この数は,10a+bと表される.
また,十の位の数と一の位の数を入れかえてできる数は,10b+aとなる.このとき,この2数の差は,
a-b は整数なので,9(a-b) は9の倍数である.したがって,2けたの正の整数と,その数の十の位と一の位の数を入れかえてできる数との差は,9の倍数である.
また,十の位の数と一の位の数を入れかえてできる数は,10b+aとなる.このとき,この2数の差は,
|
|
a-b は整数なので,9(a-b) は9の倍数である.したがって,2けたの正の整数と,その数の十の位と一の位の数を入れかえてできる数との差は,9の倍数である.
| (1) | 余白に記入 |
@2026 http://sugaku.club/