三平方の定理
定期試験対策テスト 時間 50分 1/11 ページ
点
1
次の問に答えなさい.
1
2点×4
| (1) | |
| (2) | |
| (3) | |
| (4) |
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 2/11 ページ
2
次の問に答えなさい. [380-00]
2
11点 部分点可
次の図のように,∠C=90°の直角三角形ABCの頂点Cから,斜辺ABに垂線CDをひくと,
△ABC∽△CBD
△ABC∽△ACD
であることから,a2+b2=c2となることを証明しなさい.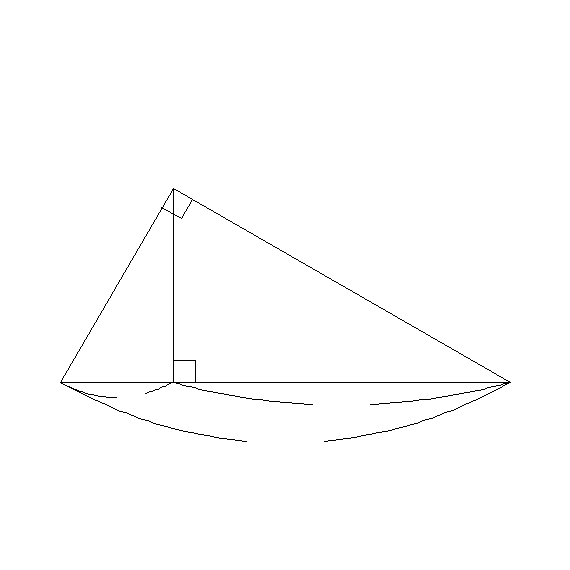
△ABC∽△CBD
△ABC∽△ACD
であることから,a2+b2=c2となることを証明しなさい.
A
B
C
D
a
b
c
y
x
| 空欄に記入 |
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 3/11 ページ
3
次の問に答えなさい.
3
2点×4
| (1) | |
| (2) | |
| (3) | |
| (4) |
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 4/11 ページ
4
次の問に答えなさい.
4
3点×3
(1) 半径7cmの円があります.円Oの弦ABの長さが,8cmのとき,中心Oから弦ABまでの距離を求めなさい. [393-00]
O
A
B
H
| cm | |||
| 8 | |||
| (1) | |
| (2) | |
| (3) |
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 5/11 ページ
5
次の問に答えなさい.
5
4点×2
| (1) | |
| (2) |
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 6/11 ページ
6
次の問に答えなさい.
6
4点×2
| (1) | |
| (2) |
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 7/11 ページ
7
次の問に答えなさい.
7
3点×3
次の図は直方体です.次の問に答えなさい. [3A0-00]
1.ACの長さを AB,BCを使って求めなさい.
2.AGの長さを AB,BC,CGを使って求めなさい.
3.AB=7cm ,BC=7cm ,CG=6cm のとき,AGの長さを求めなさい.
A
B
C
D
E
F
G
H
1.ACの長さを AB,BCを使って求めなさい.
2.AGの長さを AB,BC,CGを使って求めなさい.
3.AB=7cm ,BC=7cm ,CG=6cm のとき,AGの長さを求めなさい.
| 1 | |
| 2 | |
| 3 |
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 8/11 ページ
8
次の問に答えなさい.
8
3点×3
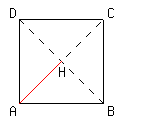
正四角錐OABCDがあります.底面ABCDは,1辺が3cm の正方形で,他の辺の長さは,すべて3cm です.次の問に答えなさい. [3A2-00]
1.AHの長さを求めなさい.
2.OHの長さを求めなさい.
3.OABCDの体積を求めなさい.
A
B
C
D
O
H
3cm
3cm
1.AHの長さを求めなさい.
2.OHの長さを求めなさい.
3.OABCDの体積を求めなさい.
| 1 | |
| 2 | |
| 3 |
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 9/11 ページ
9
次の問に答えなさい. [3A3-20]
9
9点 部分点可
底面が半径 3cm の円形で,母線の長さが,7cm である円錐の体積を求めなさい.
A
O
H
7cm
3cm
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 10/11 ページ
10
次の問に答えなさい. [3A4-10]
10
9点 部分点可
次の図の直角三角形ABCを,直線 l のまわりに1回転させてできる立体の体積を求めなさい.
A
l
B
C
7cm
2cm
@2026 http://sugaku.club/
三平方の定理
定期試験対策テスト 11/11 ページ
11
次の問に答えなさい. [3A4-00]
11
6点×2
次の図は,底面の1辺が,3cm,高さが,5cmの正四角柱です.頂点Aから頂点Eまで,糸を最短距離でかけます.次の問に答えなさい.
1.かけた糸を,下の展開図に描きなさい.
2.糸の長さを求めなさい.
A
B
C
D
E
F
G
H
1.かけた糸を,下の展開図に描きなさい.
2.糸の長さを求めなさい.
| 1 | 図に記入 |
| 2 |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 時間 50分 1/11 ページ
1
次の問に答えなさい.
1
2点×4
(4) 次の長さを3辺とする三角形のうち,直角三角形はどれですか. [382-00]
| (ア) | |||||||
| 4 | , | 5 | , | 6 | |||
| (イ) |
| |||||||||||
| 2 | , | , | 3 | |||||||||
| (ウ) |
|
| |||||||||||||||
| 2 | , | , | |||||||||||||||
| (エ) |
|
| |||||||||||||||
| , | 1 | , | |||||||||||||||
| (ア) |
|
|
| ||||||||||||||||||
| 4 | + | 5 | = | 41 | ≠ | 6 | |||||||||||||||
| (イ) |
|
|
|
| ◯ | |||||||||||||||||||
| 2 | + | = | 3 | |||||||||||||||||||||
| (ウ) |
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
| 2 | + | = | ≠ | |||||||||||||||||||||||||||||||||||||
| (エ) |
|
|
|
|
| ◯ | |||||||||||||||||||||||
| + | 1 | = | |||||||||||||||||||||||||||
| (1) |
|
||||||||||||
| (2) |
|
||||||||||||
| (3) |
|
||||||||||||
| (4) | イ ,エ |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 2/11 ページ
2
次の問に答えなさい. [380-00]
2
11点 部分点可
次の図のように,∠C=90°の直角三角形ABCの頂点Cから,斜辺ABに垂線CDをひくと,
△ABC∽△CBD
△ABC∽△ACD
であることから,a2+b2=c2となることを証明しなさい. △ABC∽△CBDだから
△ABC∽△CBDだから
AB:CB=BC:BD
c : a = a : y
よって, a2=cy ---①
△ABC∽△ACDだから
AB:AC=AC:AD
c : b = b : x
よって, b2=cx ---②
① ② から,
c=x+yだから
△ABC∽△CBD
△ABC∽△ACD
であることから,a2+b2=c2となることを証明しなさい.
A
B
C
D
a
b
c
y
x
AB:CB=BC:BD
c : a = a : y
よって, a2=cy ---①
△ABC∽△ACDだから
AB:AC=AC:AD
c : b = b : x
よって, b2=cx ---②
① ② から,
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| |||||||||||||||||
| a | + | b | = | c | |||||||||||||||
| 空欄に記入 |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 3/11 ページ
3
次の問に答えなさい.
3
2点×4
| (2) 2辺の長さが |
|
| の三角形があります. | ||||||||||||||
| cm | , | cm | |||||||||||||||
残りの1辺の長さをx cm とする.
|
|
| (1) |
|
||||||||||||||||||||||||
| (2) |
|
||||||||||||||||||||||||
| (3) |
|
||||||||||||||||||||||||
| (4) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 4/11 ページ
4
次の問に答えなさい.
4
3点×3
(1) 半径7cmの円があります.円Oの弦ABの長さが,8cmのとき,中心Oから弦ABまでの距離を求めなさい. [393-00]
OHを x とすると.
x>0 だから
O
A
B
H
| cm | |||
| 8 | |||
| cm | |||
| 7 | |||
x
|
|
| |||||||||||||||||
| AO | = | OH | + | AH | |||||||||||||||
|
|
| |||||||||||||||||||
| x | = | 7 | − | 4 | = | 33 | |||||||||||||||
| ||||||||||
| x | = | |||||||||
| (2) 1辺の長さが |
| の | ||||||
B
A
C
| ||||||||
| h | |||
| 1 |
| ||||||||
| 2 | |||||||||
|
|
| 1 |
|
| 15 | ||||||||||||||||||||||||||||
| h | = | − | ( | ) | = | |||||||||||||||||||||||||||||
| 2 | 4 | |||||||||||||||||||||||||||||||||
| h>0 だから | 1 |
| |||||||||
| h | = | ||||||||||
| 2 | |||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
(3) 次の座標を持つ2点の間の距離を求めなさい. [394-01]
AB>0 だから
| A | ( | 1 | , | 1 | ) | , | B | ( | 2 | , | 2 | ) | |||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||
| AB | = | |||||||||
| (1) |
|
||||||||||||||
| (2) |
|
||||||||||||||
| (3) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 5/11 ページ
5
次の問に答えなさい.
5
4点×2
(2) xの値を求めなさい. [396-00]

頂点CからABに垂線を引き,その交点をHとする.
△CBHは,30°,60°,90°の直角三角形だから,
△CAHは,45°,45°,90°の直角二等辺三角形だから,
A
45°
B
x
| 4 | |||
C
H
30°
45°
60°
△CBHは,30°,60°,90°の直角三角形だから,
| CH | = | 2 | |||
| |||||||||||
| x | = | 2 | |||||||||
| (1) |
|
|||||||||||||||
| (2) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 6/11 ページ
6
次の問に答えなさい.
6
4点×2
(1) xの値を求めなさい. [397-10]

直角三角形ABHについて,
直角三角形ACHについて,
x>0 だから
A
B
C
H
x
| |||||||||
| 2 | |||||||||
| 2 | |||
| 4 | |||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||
| x | = | 4 | |||||||||
(2) xの値を求めなさい. [397-00]

直角三角形ABHについて,
直角三角形ACHについて,
x>0 だから
A
B
C
H
| |||||||||
| 2 | |||||||||
x
| 6 | |||
| 2 | |||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||
| x | = | 2 | |||||||||
| (1) |
|
|||||||||||||||
| (2) |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 7/11 ページ
7
次の問に答えなさい.
7
3点×3
次の図は直方体です.次の問に答えなさい. [3A0-00]
1.ACの長さを AB,BCを使って求めなさい.
△ABCの直角三角形から
AC>0 だから
2.AGの長さを AB,BC,CGを使って求めなさい.
△ACGに着目すると,∠ACG=90°だから
①より
AG>0 だから
3.AB=7cm ,BC=7cm ,CG=6cm のとき,AGの長さを求めなさい.
A
B
C
D
E
F
G
H
1.ACの長さを AB,BCを使って求めなさい.
△ABCの直角三角形から
|
|
| ---① | ||||||||||||||||
| AC | = | AB | + | BC | |||||||||||||||
| ||||||||||||||||||||||||||||
| AC | = | |||||||||||||||||||||||||||
2.AGの長さを AB,BC,CGを使って求めなさい.
△ACGに着目すると,∠ACG=90°だから
|
|
| |||||||||||||||||
| AG | = | AC | + | CG | |||||||||||||||
|
|
|
| ||||||||||||||||||||||
| AG | = | AB | + | BC | + | CG | |||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||
| AG | = | |||||||||||||||||||||||||||||||||||||||
3.AB=7cm ,BC=7cm ,CG=6cm のとき,AGの長さを求めなさい.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| 1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
| 2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
| 3 |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 8/11 ページ
8
次の問に答えなさい.
8
3点×3
正四角錐OABCDがあります.底面ABCDは,1辺が3cm の正方形で,他の辺の長さは,すべて3cm です.次の問に答えなさい. [3A2-00]
1.AHの長さを求めなさい.
 正方形ABCDの対角線ACの長さは,
正方形ABCDの対角線ACの長さは,
正方形ABCDの対角線は,中点で交わるから,AHの長さは
2.OHの長さを求めなさい.
△OAHに着目すると,∠AHO=90°だから
OH>0 だから
3.OABCDの体積を求めなさい.
正四角錐OABCDの体積をVとすると,
A
B
C
D
O
H
3cm
3cm
1.AHの長さを求めなさい.
 正方形ABCDの対角線ACの長さは,
正方形ABCDの対角線ACの長さは,
| |||||||||||
| AC | = | AB | |||||||||
|
|
|||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
|
2.OHの長さを求めなさい.
△OAHに着目すると,∠AHO=90°だから
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
3.OABCDの体積を求めなさい.
正四角錐OABCDの体積をVとすると,
|
|
||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
| 1 |
|
||||||||||||||
| 2 |
|
||||||||||||||
| 3 |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 9/11 ページ
9
次の問に答えなさい. [3A3-20]
9
9点 部分点可
底面が半径 3cm の円形で,母線の長さが,7cm である円錐の体積を求めなさい.
[OHの長さ(円錐の高さ)を求める]
OH>0 だから
[円錐の体積を求める]
円錐の体積をVとすると,
A
O
H
7cm
3cm
[OHの長さ(円錐の高さ)を求める]
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||
| OH | = | 2 | |||||||||
[円錐の体積を求める]
円錐の体積をVとすると,
| 1 | だから | ||||||||
| V | = | × | 底面積 | × | 高さ | ||||
| 3 | |||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 10/11 ページ
10
次の問に答えなさい. [3A4-10]
10
9点 部分点可
次の図の直角三角形ABCを,直線 l のまわりに1回転させてできる立体の体積を求めなさい.
[CBの長さ(円錐の高さ)を求める]
AC>0 だから
[円錐の体積を求める]
円錐の体積をVとすると,
A
l
B
C
7cm
2cm
[CBの長さ(円錐の高さ)を求める]
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||
| CB | = | 3 | |||||||||
[円錐の体積を求める]
円錐の体積をVとすると,
| 1 | だから | ||||||||
| V | = | × | 底面積 | × | 高さ | ||||
| 3 | |||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 11/11 ページ
11
次の問に答えなさい. [3A4-00]
11
6点×2
次の図は,底面の1辺が,3cm,高さが,5cmの正四角柱です.頂点Aから頂点Eまで,糸を最短距離でかけます.次の問に答えなさい.
1.かけた糸を,下の展開図に描きなさい.
最短距離で糸をかけるから,展開図上では 直線になる.展開図上の点Pは,正四角柱における頂点Eです.また,展開図上の点Qは,正四角柱における頂点Aです.
2.糸の長さを求めなさい.
△APQに着目すると,∠AQP=90°だから
より
AP>0 だから
A
B
C
D
E
F
G
H
1.かけた糸を,下の展開図に描きなさい.
最短距離で糸をかけるから,展開図上では 直線になる.展開図上の点Pは,正四角柱における頂点Eです.また,展開図上の点Qは,正四角柱における頂点Aです.
2.糸の長さを求めなさい.
△APQに着目すると,∠AQP=90°だから
|
|
| |||||||||||||||||
| AP | = | AQ | + | PQ | |||||||||||||||
| AQ | = | 4 | × | 3 | = | 12 | |||
| PQ | = | 5 | |||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
| AP | = | 13 | |||
| 1 | 図に記入 | |||||||||
| 2 |
|
@2026 http://sugaku.club/