相似
定期試験対策テスト 時間 50分 1/11 ページ
点
1
次の問に答えなさい. [2V3-00]
1
1点×6
四角形ABCDと四角形EFGHは相似である.対応する角と辺を答えなさい.
| 1. ∠Cに対応する角 2. ∠Hに対応する角 3. ∠Aに対応する角 4. 辺DAに対応する辺 5. 辺EFに対応する辺 6. 四角形ABCDと四角形EFGHが相似である関係を記号で書きなさい | C 125° D A 75° B 75° G H 85° E F |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
2
下図の三角形の中から相似な三角形の組を選び,記号∽を使って表しなさい.また,相似条件を書きなさい. [2W1-00]
2
順不同 2点×3
3 65° A B 65° C | 6 65° D 3 E F | 5.4 65° G 2.7 H I |
7 J 5 K 6 L | 2.7 65° M N 65° O | 4.9 P 3.5 Q 4.2 R |
| (1) | |
| (2) | |
| (3) |
@2026 http://sugaku.club/
相似
定期試験対策テスト 2/11 ページ
3
次の問に答えなさい. [2V1-00]
3
2点
△ABCと△DEFは相似です.次の問に答えなさい.
| BC=19cm,EF=31cmです.△ABCと△DEFは相似比を求めなさい. | A B C D E F |
4
次の問に答えなさい. [2V2-00]
4
2点
△ABCと△DEFは相似です.次の問に答えなさい.
| AB=13cm,DE=18cmです. BC=11cmのとき,EFの大きさを求めなさい. | A B C D E F |
@2026 http://sugaku.club/
相似
定期試験対策テスト 3/11 ページ
5
次の問に答えなさい.
5
3点×3
| (1) | |
| (2) | |
| (3) |
@2026 http://sugaku.club/
相似
定期試験対策テスト 4/11 ページ
6
次の問に答えなさい. [2X0-00]
6
10点 部分点可
次の図で,AD//BCならば△AOD∽△COBであることを証明しなさい.
A
B
C
D
O
| 余白に記入 |
@2026 http://sugaku.club/
相似
定期試験対策テスト 5/11 ページ
7
次の問に答えなさい. [2X2-00]
7
10点 部分点可
次の図で,△ABCは,正三角形です.AC上に点Dがあります.BDを一辺とする正三角形BDEをつくるとき,△BCD∽△BEFであることを証明しなさい.また,DEとABの交点をFとする.
A
B
C
D
E
F
| 余白に記入 |
@2026 http://sugaku.club/
相似
定期試験対策テスト 6/11 ページ
8
次の問に答えなさい. [2Y7-00]
8
10点 部分点可
△ABCで,∠Aの二等分線と辺BCとの交点をDとするとき,AB:AC=BD:DCが成り立つことを証明しなさい.ただし,点Cを通り,DAに平行な直線と,BAを延長した直線との交点をEとする.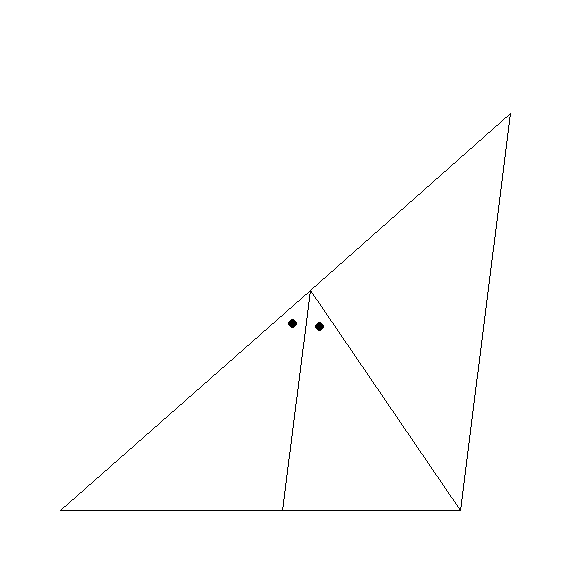
C
A
B
D
E
| 余白に記入 |
@2026 http://sugaku.club/
相似
定期試験対策テスト 7/11 ページ
9
次の問に答えなさい.
9
(2)完答6点 他3点×2
| (1) | |
| (2) | |
| (3) |
@2026 http://sugaku.club/
相似
定期試験対策テスト 8/11 ページ
10
次の問に答えなさい. [2Y6-00]
10
4点×2
次の平行四辺形ABCDで,AB上の点Eが ,AE:EB=1:2の位置にあり,BC上の点Fが ,BF:FC=1:1の位置にある.ACとDEの交点をP,ACとDFの交点をQとする.次の問に答えなさい.
 1. AP:PQ:QC を最も簡単な整数の比で表しなさい.
1. AP:PQ:QC を最も簡単な整数の比で表しなさい.
2. AC=36cm のとき,PQの長さを求めなさい.
A
B
C
D
E
F
P
Q
2. AC=36cm のとき,PQの長さを求めなさい.
| 1 | |
| 2 |
@2026 http://sugaku.club/
相似
定期試験対策テスト 9/11 ページ
11
次の問に答えなさい.
11
3点×3
O
A
B
P
Q
| (1) | |
| (2) | |
| (3) |
@2026 http://sugaku.club/
相似
定期試験対策テスト 10/11 ページ
12
次の問に答えなさい.
12
3点×4
(3) 図の立体は,OAを母線として,Hを中心とする円Hを底面とした円錐です.これを円錐Pとします.また図のように,円Hに平行な Gを含む平面で円錐Pから立体を切り取ります.この切り取った円錐を円錐Qとします.GはOH上の点で,OG:GH=3:2の関係があります.円錐Pの体積Vpは,5000m3です. [315-00]
| 1. 円錐Pと円錐Qの相似比を求めなさい. 2. 円錐Qの体積Vqを求めなさい. |
| (1) | |
| (2) | |
| (3) 1 |
|
| (3) 2 |
@2026 http://sugaku.club/
相似
定期試験対策テスト 11/11 ページ
13
次の問に答えなさい.
13
4点
(1) 校庭の木の高さを求めるため,根本から30m 離れた場所に立ち,木の先端を見上げた時の水平面からの角度を測定した.その角度をA°,測定者の目の高さを160cmとする.続いて,一角がA°となる直角三角形を描き,辺の長さを図ると次の図のようになった.木の高さを求めなさい. [320-00]

| (1) |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 時間 50分 1/11 ページ
1
次の問に答えなさい. [2V3-00]
1
1点×6
四角形ABCDと四角形EFGHは相似である.対応する角と辺を答えなさい.
| 1. ∠Cに対応する角 2. ∠Hに対応する角 3. ∠Aに対応する角 4. 辺DAに対応する辺 5. 辺EFに対応する辺 6. 四角形ABCDと四角形EFGHが相似である関係を記号で書きなさい | C 125° D A 75° B 75° G H 85° E F |
| 1 | ∠G |
| 2 | ∠D |
| 3 | ∠E |
| 4 | 辺HE |
| 5 | 辺AB |
| 6 | 四角形ABCD∽四角形EFGH |
2
下図の三角形の中から相似な三角形の組を選び,記号∽を使って表しなさい.また,相似条件を書きなさい. [2W1-00]
2
順不同 2点×3
3 65° A B 65° C | 6 65° D 3 E F | 5.4 65° G 2.7 H I |
7 J 5 K 6 L | 2.7 65° M N 65° O | 4.9 P 3.5 Q 4.2 R |
| (1) | △JKL∽△PQR 3組の辺の比がすべて等しい. |
| (2) | △DEF∽△GHI 2組の辺の比とその間の角がそれぞれ等しい. |
| (3) | △ABC∽△MNO 2組の角がそれぞれ等しい. |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 2/11 ページ
3
次の問に答えなさい. [2V1-00]
3
2点
△ABCと△DEFは相似です.次の問に答えなさい.
| BC=19cm,EF=31cmです.△ABCと△DEFは相似比を求めなさい. 対応する1組の辺の長さの比が相似比に等しいので
| A B C D E F |
|
4
次の問に答えなさい. [2V2-00]
4
2点
△ABCと△DEFは相似です.次の問に答えなさい.
| AB=13cm,DE=18cmです. BC=11cmのとき,EFの大きさを求めなさい.
| A B C D E F |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 3/11 ページ
5
次の問に答えなさい.
5
3点×3
A
B
E
D
C
x
7
7.5
10.5
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| (1) | 7 | |||||||||
| (2) |
|
|||||||||
| (3) | 5 |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 4/11 ページ
6
次の問に答えなさい. [2X0-00]
6
10点 部分点可
次の図で,AD//BCならば△AOD∽△COBであることを証明しなさい.
△AODと△COBにおいて
仮定より AD//BC
錯角は等しいから
∠OAD=∠OCB
∠ODA=∠OBC
2組の角がそれぞれ等しい ので
△AOD∽△COB
A
B
C
D
O
△AODと△COBにおいて
仮定より AD//BC
錯角は等しいから
∠OAD=∠OCB
∠ODA=∠OBC
2組の角がそれぞれ等しい ので
△AOD∽△COB
| 余白に記入 |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 5/11 ページ
7
次の問に答えなさい. [2X2-00]
7
10点 部分点可
次の図で,△ABCは,正三角形です.AC上に点Dがあります.BDを一辺とする正三角形BDEをつくるとき,△BCD∽△BEFであることを証明しなさい.また,DEとABの交点をFとする.
△BCDと△BEFにおいて
△ABCと△BDEは,正三角形だから
∠BCD=∠BEF=60° ---①
∠CBA=∠DBE=60° ---②
また,
∠CBA=∠CBD+∠DBF
∠DBE=∠EBF+∠DBF
したがって,②より
∠CBD=∠EBF ---③
① ③ から,2組の角がそれぞれ等しい ので
△BCD∽△BEF
A
B
C
D
E
F
△BCDと△BEFにおいて
△ABCと△BDEは,正三角形だから
∠BCD=∠BEF=60° ---①
∠CBA=∠DBE=60° ---②
また,
∠CBA=∠CBD+∠DBF
∠DBE=∠EBF+∠DBF
したがって,②より
∠CBD=∠EBF ---③
① ③ から,2組の角がそれぞれ等しい ので
△BCD∽△BEF
| 余白に記入 |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 6/11 ページ
8
次の問に答えなさい. [2Y7-00]
8
10点 部分点可
△ABCで,∠Aの二等分線と辺BCとの交点をDとするとき,AB:AC=BD:DCが成り立つことを証明しなさい.ただし,点Cを通り,DAに平行な直線と,BAを延長した直線との交点をEとする.
AD//ECより,平行線の同位角は等しいので,
∠BAD=∠AEC
また,錯角は等しいので,
∠DAC=∠ACE
仮定より,
∠BAD=∠DAC
したがって,
∠AEC=∠ACE
△ACEは,2つの角が等しいから二等辺三角形となり
AE=AC ---①
△BECで,AD//ECから,
BA:AE=BD:DC ---②
① ② から,
AB:AC=BD:DC
C
A
B
D
E
AD//ECより,平行線の同位角は等しいので,
∠BAD=∠AEC
また,錯角は等しいので,
∠DAC=∠ACE
仮定より,
∠BAD=∠DAC
したがって,
∠AEC=∠ACE
△ACEは,2つの角が等しいから二等辺三角形となり
AE=AC ---①
△BECで,AD//ECから,
BA:AE=BD:DC ---②
① ② から,
AB:AC=BD:DC
| 余白に記入 |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 7/11 ページ
9
次の問に答えなさい.
9
(2)完答6点 他3点×2
(2) 直線 k,l,m,n が平行のとき,x,y を計算しなさい. [2Y4-00]
10
5
15
y
6
x
k
l
m
n
|
|
| (1) |
|
|||||||||||||||||||||||||||
| (2) |
|
|||||||||||||||||||||||||||
| (3) | 6 |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 8/11 ページ
10
次の問に答えなさい. [2Y6-00]
10
4点×2
次の平行四辺形ABCDで,AB上の点Eが ,AE:EB=1:2の位置にあり,BC上の点Fが ,BF:FC=1:1の位置にある.ACとDEの交点をP,ACとDFの交点をQとする.次の問に答えなさい.
 1. AP:PQ:QC を最も簡単な整数の比で表しなさい.
1. AP:PQ:QC を最も簡単な整数の比で表しなさい.
AE//CDから △AEP∽△CDP,したがって
AD//CFから △AQD∽△CQF,したがって
AP:PC と AQ:QC の AC が共通なので AC の値をそろえる.
したがって
2. AC=36cm のとき,PQの長さを求めなさい.
A
B
C
D
E
F
P
Q
AE//CDから △AEP∽△CDP,したがって
| AE | : | CD | = | AP | : | PC | = | 1 | : | 3 | |||
AD//CFから △AQD∽△CQF,したがって
| AD | : | CF | = | AQ | : | QC | = | 2 | : | 1 | |||
AP:PC と AQ:QC の AC が共通なので AC の値をそろえる.
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. AC=36cm のとき,PQの長さを求めなさい.
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
| 1 |
|
|||||||||||||||||||||||||||||||||||||||
| 2 | 15cm |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 9/11 ページ
11
次の問に答えなさい.
11
3点×3
(2) 相似な図形A,Bがあります.相似比は,A:B=3:5 です.Aの面積が72m2のときBの面積を求めなさい. [302-00]
相似比が m:nの相似図形の面積比は,m2:n2. 図形Aの面積をSa,図形Bの面積をSbとすると
相似比が m:nの相似図形の面積比は,m2:n2. 図形Aの面積をSa,図形Bの面積をSbとすると
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
O
A
B
P
Q
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| (1) |
|
|||||||||||||||
| (2) |
|
|||||||||||||||
| (3) | 50cm2 |
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 10/11 ページ
12
次の問に答えなさい.
12
3点×4
(1) 相似な図形A,Bがあります.Aの表面積は,10cm2.Bの表面積は,360cm2のとき相似比A:Bを求めなさい. [311-00]
相似比が m:nの相似図形の表面積比は,m2:n2. 図形Aと図形Bの表面積比をA2:B2とすると
相似比が m:nの相似図形の表面積比は,m2:n2. 図形Aと図形Bの表面積比をA2:B2とすると
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
(2) 相似な立体図形A,Bがあります.相似比は,A:B=5:2 です.Aの体積が125cm3のときBの体積を求めなさい. [313-00]
相似比が m:nの相似図形の体積比は,m3:n3. 図形Aの体積をVa,図形Bの体積をVbとすると
相似比が m:nの相似図形の体積比は,m3:n3. 図形Aの体積をVa,図形Bの体積をVbとすると
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
(3) 図の立体は,OAを母線として,Hを中心とする円Hを底面とした円錐です.これを円錐Pとします.また図のように,円Hに平行な Gを含む平面で円錐Pから立体を切り取ります.この切り取った円錐を円錐Qとします.GはOH上の点で,OG:GH=3:2の関係があります.円錐Pの体積Vpは,5000m3です. [315-00]
| 1. 円錐Pと円錐Qの相似比を求めなさい. 相似比は,対応する1組の辺の長さの比に等しいので
|
| (1) |
|
|||||||||||||||||||||||||||
| (2) |
|
|||||||||||||||||||||||||||
| (3) 1 |
|
|||||||||||||||||||||||||||
| (3) 2 |
|
@2026 http://sugaku.club/
【解答例】
定期試験対策テスト 11/11 ページ
13
次の問に答えなさい.
13
4点
(1) 校庭の木の高さを求めるため,根本から30m 離れた場所に立ち,木の先端を見上げた時の水平面からの角度を測定した.その角度をA°,測定者の目の高さを160cmとする.続いて,一角がA°となる直角三角形を描き,辺の長さを図ると次の図のようになった.木の高さを求めなさい. [320-00]


|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
| (1) | 30.6m |
@2026 http://sugaku.club/